LA TEMPERATURA DI EQUILIBRIO

Finora, dice l’insegnante, abbiamo parlato di temperatura T* della miscela che risulta essere sempre maggiore di T1 e minore di T2:

Noi non sappiamo rispondere.
L’insegnante allora disegna sulla lavagna due recipienti cilindrici uguali, che chiama vasi, comunicanti tra loro per mezzo di un tubo munito di un rubinetto il quale se aperto consente la comunicazione, se chiuso la interrompe.
L’insegnante ci fa supporre che inizialmente il rubinetto sia chiuso e che vengono versate nei due vasi quantità diverse di acqua come indicato nella figura 1.

fig.1                                                                                  fig.2

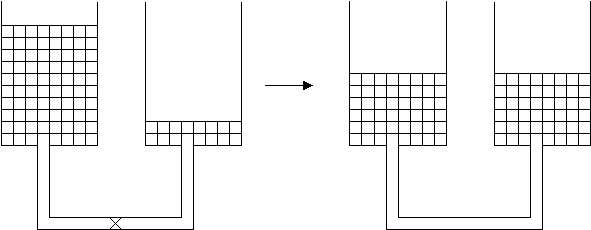
Nel vaso 1 il livello raggiunto dall’acqua (livello A) è maggiore del livello raggiunto dall’acqua (livello B) nel vaso 2.

A questo punto l’insegnante ci domanda:
"Immaginando di aprire il rubinetto, cosa pensate possa succedere?"
Noi abbiamo risposto che nel momento in cui il rubinetto viene aperto l’acqua andrà dal vaso 1 al vaso 2.
Fino a quando – domanda allora l’insegnante – l’acqua tenderà a fluire dal vaso 1 al vaso 2?
Noi abbiamo risposto:
"Fino a quando il livello dell’acqua contenuta nel vaso 1 non sarà uguale a quello dell’acqua contenuta nel vaso 2". (figura 2)
L’insegnante ci dice che la nostra risposta è corretta e aggiunge che, nel momento in cui il livello dell’acqua nel vaso 1 risulta uguale al livello dell’acqua nel vaso 2, viene raggiunto uno stato di equilibrio.
Come si intuisce, e come si vede anche dalla figura 2, il livello (livello C) raggiunto dall’acqua nei due vasi nel momento in cui viene raggiunto l’ equilibrio è inferiore al livello A e superiore al livello B.

fig.3                                                                                fig. 4
 
 
 
 

L’insegnante ci domanda:
"Aprendo il rubinetto, cosa pensate possa succedere?".
Noi abbiamo risposto che anche in questo caso, nel momento in cui il rubinetto viene aperto, l’acqua andrà dal vaso 1 dove il livello è maggiore al vaso 2 dove il livello è minore,fino a quando il livello dell’acqua nel vaso 1 non sarà uguale al livello dell’acqua nel vaso 2. (figura 4)

L’insegnante ci domanda:
"Se un quadretto rappresenta ad esempio 20 ml, quanta acqua è contenuta nel vaso 1 e quanta nel vaso 2?".
Noi abbiamo contato il numero di quadretti contenuti nel vaso 1; essi sono 45; poi abbiamo eseguito la moltiplicazione:
20 ml x 45 = 900 ml
quindi nel vaso 1 sono contenuti 900 ml di acqua.

Abbiamo ripetuto lo stesso procedimento contando il numero di quadretti contenuti nel vaso 2; anch’essi sono 45 e quindi anche nel vaso 2 sono contenuti 900 ml di acqua.
Abbiamo scoperto che nei due vasi è contenuta la stessa quantità di acqua.
Concludiamo quindi che l’acqua, pur essendo contenuta in quantità uguali nei vasi 1 e 2, poiché raggiunge livelli diversi, quando il rubinetto è aperto fluisce dal vaso 1 dove raggiunge un livello maggiore al vaso 2 dove raggiunge un livello minore fino a quando il livello raggiunto nei vasi 1 e 2 sarà lo stesso.

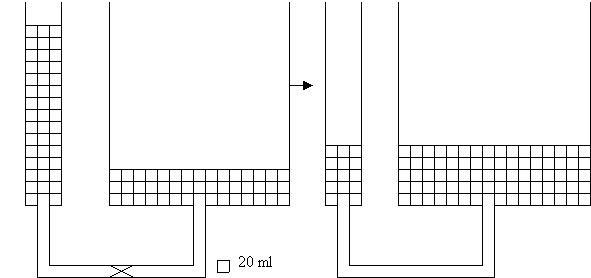
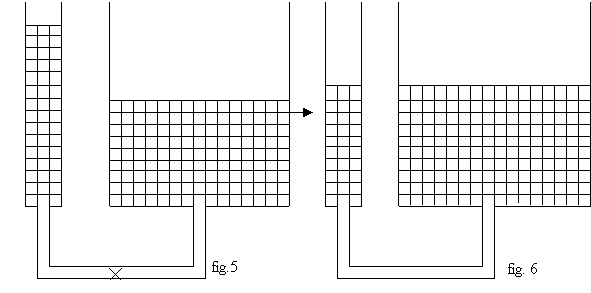
Ora l’insegnante considera di nuovo i due vasi e suppone di versare nel vaso 1 una certa quantità di acqua, ad esempio 90 ml, e nel vaso 2 una quantità maggiore, ad esempio tripla e quindi uguale a 270 ml, schematizzando la situazione come nella figura 5. 

Dalla rappresentazione grafica si osserva che, nonostante la quantità di acqua nel vaso 1 sia minore di quella contenuta nel vaso 2, il livello (livello A) raggiunto dall’acqua nel vaso 1 è maggiore di quello (livello B) raggiunto nel vaso 2.

Quindi ci domanda:
"Aprendo il rubinetto, il flusso dell’acqua quale direzione avrà?"
Noi abbiamo risposto che l’acqua tenderà ad andare dal vaso 1 dove il livello è maggiore al vaso 2 dove il livello è minore in modo che nei due vasi l’acqua raggiunga uno stesso livello (livello C) ed abbiamo schematizzato la situazione come appare nella figura 6. 
L’insegnante ha detto che il nostro ragionamento è corretto ed ha fatto presente che, anche se l’acqua è presente in maggior quantità nel vaso 2 tuttavia, poiché il livello raggiunto dall’acqua nel vaso 1, a causa della sua forma, è maggiore di quello raggiunto nel vaso 2, essa fluisce dal vaso 1 al vaso 2.

Dopo queste considerazioni concludiamo che è il livello diverso che determina la direzione del flusso di acqua e non la quantità.
Ora supponiamo – continua l’insegnante – che in due vasi, vaso 1 e vaso 2, aventi le stesse dimensioni e fra i quali la comunicazione sia inizialmente interrotta, siano versate due quantità uguali di acqua aventi temperature T1 e T2 diverse; ad esempio T1 uguale a 80°C e T2 uguale a quella ambiente, ad esempio 20°C. (figura 7)
Fra le due quantità di acqua esiste un dislivello di temperatura in quanto T1 è maggiore di T2. Possiamo schematizzare meglio i diversi livelli di temperatura e di calore nel modo seguente:

(In questo caso, poiché le quantità di acqua sono uguali, ad una temperatura maggiore corrisponde una quantità di calore maggiore, per cui l’acqua contenuta nel vaso 1 possiede una quantità di calore Q1 maggiore della quantità di calore Q2 posseduta dall’acqua contenuta nel vaso 2).

Supponiamo di aprire il rubinetto per consentire la comunicazione tra i due vasi. (figura 9)

Tra due corpi, uno caldo ed uno freddo, il calore passa dal corpo più caldo a quello più freddo, cioè da quello avente temperatura più alta a quello avente temperatura più bassa fino a quando i due corpi non raggiungono la stessa temperatura. Nel caso in esame il calore tenderà a passare dall’acqua contenuta nel vaso 1,avente temperatura T1 maggiore, all’acqua contenuta nel vaso 2 avente temperatura T2 minore con conseguente diminuzione di T1 ed aumento di T2 fino al momento in cui la temperatura (T*) dell’acqua contenuta nei vasi 1 e 2 avrà lo stesso valore. 
La temperatura finale T* sarà:

Fra le due bambine, è evidente, non c’è una "distribuzione equilibrata" di caramelle; per raggiungere un equilibrio nella distribuzione delle caramelle alcune devono "fluire", cioè passare, da Maria ad Elena fino a quando entrambe le bambine non ne abbiano lo stesso numero.

Immaginiamo che questo passaggio di caramelle da Maria ad Elena avvenga gradualmente e che inizi con il trasferimento di una; risulterà che Maria ne possiederà sei ed Elena quattro: il "dislivello" di caramelle fra le due bambine è diminuito. Con il successivo passaggio di un’altra caramella da Maria ad Elena entrambe le bambine verranno ad avere lo stesso numero di caramelle, cioè cinque: il dislivello è annullato e si è raggiunto uno stato di equilibrio.

Posso giungere a tale risultato, cioè calcolare il numero di caramelle che ciascuna bambina possiederà nel momento in cui viene raggiunto l’equilibrio pensando, invece che al trasferimento (o flusso o passaggio) di caramelle, di mettere quest’ultime in un unico contenitore, di contarle e di dividere il totale per il numero di bambine fra cui le devo distribuire:

(n° caramelle di Maria + n° caramelle di Elena)/n° bambine = (7 + 3)/2 = 10/2 = 5

Pensiamo ora all’esperimento eseguito, relativo alla determinazione della temperatura T* di una miscela formata da due quantità uguali di acqua aventi una temperatura T1, e l’altra temperatura T2.
Inizialmente - vedi figura 10 - abbiamo due contenitori uguali, becher 1 e becher 2, contenenti quantità uguali di acqua aventi temperature diverse T1 e T2 con T2 > T1.

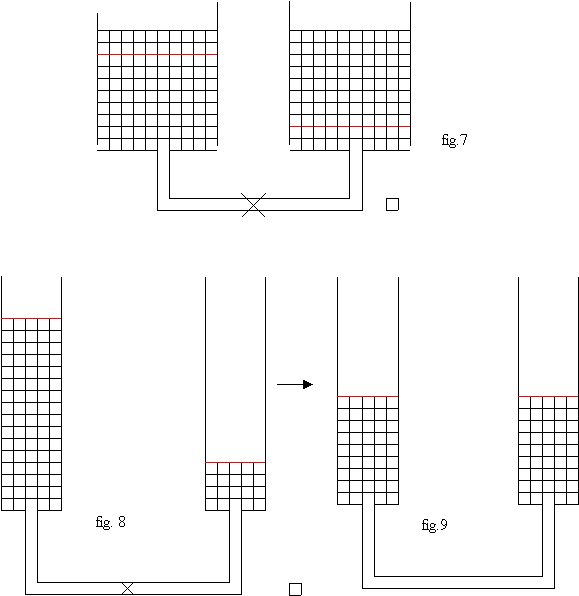
(L’acqua che si trova a temperatura T2 possiede una quantità di calore Q2 maggiore della quantità di calore Q1 posseduta dall’acqua che si trova a temperatura T1: ciò lo possiamo affermare perché le quantità di acqua sono uguali e quindi in questo caso ad una temperatura maggiore corrisponde una quantità di calore maggiore e poi, se non altro, perché l’acqua contenuta nel becher 2, avente temperatura T2, è stata posta sulla fiamma bunsen e l’altra, contenuta nel becher 1, avente temperatura T1, è stata fatta rimanere a temperatura ambiente).

Successivamente versiamo, ad esempio, l’acqua contenuta nel becher 1 nel becher 2, agitiamo velocemente e misuriamo la temperatura della miscela.

Proviamo se, schematizzando la realtà, risulta più semplice studiarla.

Supponiamo che, versando i 100 ml di acqua fredda dal becher 1 nel becher 2 contenente i 100 ml di acqua calda, le due quantità di acqua rimangano stratificate una sopra l’altra come nel modello che viene proposto nella figura 11.

Come sappiamo, fra due corpi messi a contatto il calore passa dal corpo più caldo a quello più freddo, cioè da quello avente temperatura maggiore a quello avente temperatura minore.

Nel caso specifico il calore tenderà a passare dai 100 ml di acqua la cui temperatura T1 è più elevata ai 100 ml di acqua la cui temperatura T1 è meno elevata, fino a quando ognuno dei 100 ml di acqua non avrà la stessa temperatura. Infatti mano a mano che il calore passa dai 100 ml di acqua aventi temperatura T2 più elevata ai 100 ml di acqua aventi temperatura T1 meno elevata, T2 diminuisce e T1 aumenta fino a quando la temperatura di ognuna delle due quantità di acqua avrà raggiunto uno stesso valore T* maggiore di T1 e minore di T2.

Possiamo confrontare l’esempio delle due gemelle che possiedono un numero diverso di caramelle con la realtà del nostro esperimento in cui abbiamo alla fine, all’interno di un unico becher, due uguali quantità di acqua aventi diverse temperature T1 e T2 (T2 > T1) .

Come per calcolare il numero di caramelle spettante ad ogni bambina abbiamo pensato di mettere le caramelle possedute da entrambe in un unico contenitore e di dividere il totale per 2, cioè per il numero di bambine fra cui esse devono essere ugualmente distribuite, così per calcolare la temperatura finale T* che avrà ognuna delle due quantità uguali, poiché in un unico becher si è formata una miscela dove sono presenti due diversi livelli termici, faremo:     T* = (T1 + T2)/2
La temperatura finale T* della miscela può essere allora indicata come temperatura di equilibrio perché indica la temperatura della miscela nel momento in cui viene raggiunto l’equilibrio termico, quando non c’è più passaggio di calore.