Gli esperti hanno sottoposto il gruppo a due tipi di sollecitazioni:

1.    Richiesta di realizzare esperimenti e di riflettere sui risultati.  In queste situazioni è stato osservato il comportamento di due oggetti (non sono sorgenti primarie) quando vengono accostati e si sono individuate, a regime, condizioni di equilibrio statico.

2.    Richieste di indicare andamenti di temperatura in situazioni legate all’esperienza, in modo qualitativo, spesso utilizzando grafici.  Nelle situazioni proposte si aveva un’interazione tra una sorgente primaria e un oggetto. Si sono individuate, a regime, condizioni di equilibrio stazionario.
 

I due tipi di sollecitazioni si sono alternati nel corso dei lavori, ma ora vengono commentati separatamente per chiarezza di esposizione.
 

1. Richiesta di realizzare esperimenti e di riflettere sui risultati

PROBLEMA 1
Mescolo due sostanze a due diverse temperature. Quale sarà la temperatura finale?

Vengono fatte brevi considerazioni iniziali:
1.     nel misurare la temperatura di un oggetto va tenuto conto che:

•  esso è una parte di un sistema più ampio: l’ambiente esterno. Qual è la temperatura ambiente? Quale ambiente? La situazione dell’ambiente può influenzare la misura (es: correnti d’aria, ecc.) ....
• lo strumento di misura, il termometro, va utilizzato tenendo conto che richiede un certo tempo per andare a regime (vedi problema 3), esistono problemi di taratura, si deve tener conto della sensibilità dello strumento, degli errori di misura...... 

2.     Previsione dei risultati: essendo la temperatura una variabile non additiva non si prevede di poter semplicemente sommare i valori della temperatura. Si pensa di procedere frammentado il problema e di fare misure sperimentali facendo cambiare una variabile per volta:

·       sostanze uguali, masse uguali, temperature diverse
·       sostanze uguali, masse diverse, temperature diverse
·       sostanze diverse, masse diverse, temperature diverse 

Sostanze uguali, masse uguali, temperature diverse Vengono mescolate due parti di acqua aventi la stessa massa e temperatura rispettivamente T1 e T2.
Alla richiesta di prevedere la temperatura a regime sono state fornite risposte a prima vista diverse.
La riflessione sulle risposte ha evidenziato che le formule erano solo formalmente diverse, ma che, pur portando allo stesso risultato, nascondevano modelli diversi.
a)     “faccio la media”   ha prodotto la formula    T=  (T1 + T2) / 2
alcuni dei proponenti hanno riconosciuto di aver utilizzato un modello nel quale la temperatura è associata alla lunghezza di un segmento

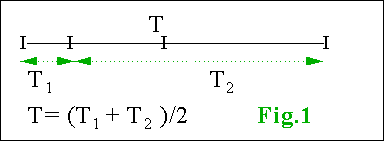
b)    “faccio la differenza delle due temperature, la divido per due e la sommo alla temperatura più bassa” ha portato alla formula       T= T1 + (T1 - T2) / 2
Ad un più attento esame è emerso che questa risposta nasconeva almeno due modelli diversi
·       l’eccesso di temperatura viene suddiviso in modo equo tra le parti (fig. 2)
·       la temperatura viene associata ad un fluido che le due parti posseggono in quantità diversa. Quando vengono messe a contatto, esso passa da uno all’altro con il modello dei vasi comunicanti, dove la differenza di livello rappresenta la differenza di temperatura tra le due masse d’acqua (fig. 3)

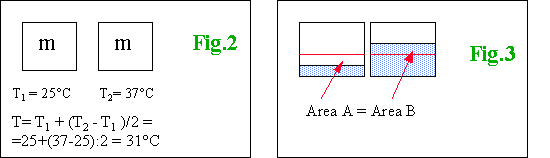
Sostanze uguali, masse diverse, temperature diverse Vengono mescolate due parti di acqua aventi rispettivamente massa m1, m2  e temperatura T1, T2
Anche in questa situazione alla richiesta di prevedere la temperatura di regime sono state fornite risposte a prima vista diverse.
La riflessione sulle risposte ha evidenziato che le formule erano solo formalmente diverse, ma che, pur portando allo stesso risultato, nascondevano modelli diversi.
1.     Si divide la somma delle masse in parti “unitarie” uguali, tra le quali divido l’eccesso di temperatura:

2.     Modello il cui lo stato iniziale dei due oggetti è rappresentato da un contenitore in cui la base rappresenta la massa e l’altezza la temperatura; la previsione della situazione a regime viene fatta con il modello dei vasi comunicanti:

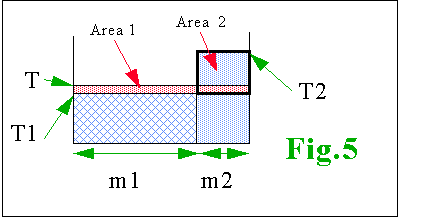
T - T1 = Area1  / (m1 + m2) = Area2  / (m1 + m2) =  m2 * (T2  - T1) / (m1 + m2)

sviluppando si ottiene:

                             T= (m1*T1 + m2*T2) / (m1 + m2)                                                                      (1)

questo modello sottointende il concetto di fluido scambiato: calorico

3.     il terzo modello presuppone la conservazione di una grandezza legata alla massa e alla variazione di temperatura: 
               m1 * DT1 = m2 * DT2                                                                                    (2)

questo modello sottointende il concetto di conservazione dell’energia ed è riconducibile all’idea di agitazione termica delle melecole

OSSERVAZIONI:

• modelli ed approcci diversi portano a risultati che dal punto di vista pratico sono equivalenti. 
• Ciò ci porta a riflettere su come certi approcci degli alunni che ci sembrano divergenti sono solo diversi dal nostro.
• mi è sembrata interessante l’osservazione che le strategie proposte si ricollegavano a due teorie sul calore storicamente proposte: quella del calorico e quella dell’agitazione termica.

Sostanze diverse, masse diverse, temperature diverse Un oggetto a temperarura ambiente T1 viene immerso in acqua avente una temperatura più alta T2
Ogni gruppo ha immerso in acqua un corpo di forma uguale, ma costituito da una diversa sostanza.
I risultati sperimentali hanno evidenziato che il tempo necessario al sistema per andare a regime dipende dal tipo di materiale immerso, inoltre i modelli precedenti non sono più in grado di descrivere la situazione: si deve tener conto di un fattore di correzione che determina la risposta del sistema legato al tipo di materiale; la formula (2) diventa:

c1 * m1 * DT1 = c2 * m2 * DT2

Si osserva che misurando le temperature iniziali e di regime si può determinare il rapporto tra i fattori di correzione dei due materiali:

c1 /c2       =      m2 * DT2 / m1 * DT1

Si introduce così il concetto di calore specifico o reciprocamente di capacità termica.

PROBLEMA 2
Metto a contatto due quantità d’acqua a due diverse temperature, interponendo una parete sottile. La temperatura a regime sarà la stessa? La storia intermedia sarà la stessa? Come influisce il materiale interposto?

Due recipienti contengono acqua ad una temperatura T1 nella prima viene immerso un bicchierino di vetro, nell’altra uno di alluminio contenenti acqua ad una temperatura T2  < T1 . Il sistema viene isolato dall’ambiente e vengono registrate le remperatura ad intervalli di 30 s .

T fuori AL (°C)	T nel bicchiere Al (°C)	T fuori vetro (°C)	T nel bicchiere vetro (°C)
22 21 22 23 23 23 23.5 24 24 24 24	54 40 36 33 31 30 29 28 27 27 27	21 23.5 24 23 24 24.5 25 25 25 25 25	51 48 44 41 38 36 33 32.5 31.5 31 30

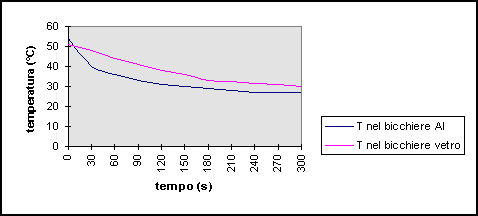
Si osserva che:

• la temperatura cala più rapidamente nel bicchierino di alluminio, è un conduttore migliore del vetro
• ci si aspetta di trovare a regime una temperatura più bassa nel bicchierino di alluminio che ha una maggiore capacità termica
• l’andamento della temperatura nel contenitore è poco significativo non avendo pensato di introdurre un agitatore

PROBLEMA 3
Che cosa misura un termometro?
La temperatura di se stesso.
Questa osservazone usualmente sottointesa comporta la necessità:
1.     di dare al termometro il tempo di andare  a regime con il corpo di cui si vuole sapere la temperatura, prima di effettuare la misura.
2.     che l’inserimento del termometro non perturbi troppo la situazione che si intende misurare.

Questa situazione si è resa evidente collegando un termometro digitale ad un computer e osservando in tempo reale il grafico delle temperature quando si prende in mano il bulbo del termometro: 

• il termometro misura inizialmente la temperatura ambiente
• nel giro di circa due minuti, il valore della temperatura sale fino a quello della mano, disegnando una curva con concavità verso il basso;
• quando il termometro viene lasciato libero nell’ambiente la temperatura cala, disegnando una curva con concavità verso l’alto,  fino alla temperatura ambiente.

PROBLEMA 4
Come varia la temperatura misurata da un termometro bagnato quando l’acqua evapora?
La temperatura continua a calare, anche sotto il valore della temperatura ambiente, fino a quando tutta l’acqua non è evaporata; a questo punto la temperatura ricomincia a salire fino a riportarsi al valore dell’ambiente .
 Con queste osservazioni si può introdurre il concetto di calore latente di evaporazione.
 

PROBLEMA 5
Come varia la temperatura nel processi di riscaldamento, fusione, raffreddamento, solidificazione di una sostanza (salolo o fenile salicilato)?
Si pone un contenitore con salolo solido su un fornello e si registra on line la temperatura del salolo fino alla completa liquefazione, poi si toglie il contenitore dal fuoco, continuando a registrare le temperature fino a completa solidificazione.
Si osservano due plateau della curva della temperatura in funzione del tempo in corrispondenza della liquefazione (il calore fornito viene utilizzato per il cambiamento di stato e la temperatura rimane costante) e della solidificazione (il salolo solidificando cede calore e la temperatura rimane costante.
Con queste osservazioni si può introdurre il concetto di calore latente di solidificazione e di fusione.

Osservazioni

L’utilizzo di sensori (temperatura, movimento, ecc.) collegati al computer permette numerose appicazioni didattiche:

• visualizzare velocemente un grafico che rappresenti l’andamento di un fenomeno
• chiedere all’alunno un grafico di previsione di un fenomeno (da fare con carta e penna) e poi proporre il confronto con la situazione reale, rappresentata sullo schermo del computer.
• ornire un grafico ottenuto da una situazione reale ed invitare gli alunni a ricreare quella particolare situazione.

Tuttavia c’è un aspetto che va gestito con cautela: per i ragazzi può non essere immediata la comprensione di grafici cartesiani in cui vengano rappresentate grandezze non legate allo spazio. Prima di rappresentare grandezze come temperatura, velocità, tempo... nel piano cartesiano bisogna portare gli alunni a comprenderne il significato. Suggerimenti utili possono essere:

• far capire con il gesto di una mano che ogni grandezza che aumenta può essere rappresentata da qualcosa che si alza;
• una volta fatto il gesto sparisce; se la mano impugna invece una matita, lascia una traccia verticale
• salite e discese successive si sovrappongono
• se la carta scorre con velocità costante, il movimento della mano dà origine ad una curva in cui la variabile orizzontale è il tempo
• osservando l’andamento della curva tracciata in diverse situazioni si può arrivare a dare significato a  forme e pendenze diverse (vedere anche punto 2 del paragrafo successivo).

Ai corsisti è stato richiesto di prevedere l’andamento della temperatura in situazioni reali, legate all’esperienza.
Le risposte sono state estremamente diverse, spesso non si sono avvicinate alla realtà. Si è osservato che:
1.   spesso quando si cerca di mettere in grafico, in modo qualitativo, l’esperienza ci si trova in difficoltà, ci si imbroglia. Si ha la tendenza a considerare il problema banale e a trascurare alcuni aspetti del fenomento.
Il suggerimento in caso di difficoltà è quello di raccontarsi una storia, ponendo attenzione alle condizioni iniziali, finali e ad eventuali punti critici intermedi.

2.   Uno degli errori più comuni è quello di un’errata valutazione della concavità della curva ‘temperatura in funzione del tempo’. L’errore viene subito riconosciuto se si riflette sul fatto che, più alta è la differenza di temperatura, maggiore è la velocità di trasferimento del calore (doppia implicazione).
Il fenomeno di trasferimento del calore tende ad auto-estinguersi:

• nell’oggetto che si scalda la temperatura aumenta sempre più piano e la curva ‘temperatura in funzione del tempo’ si avvicina ad un valore asintotico orizzontale con la concavità verso il basso.
• nell’oggetto che si raffredda la temperatura diminuisce sempre più piano e la curva ‘temperatura in funzione del tempo’ si avvicina ad un valore asintotico orizzontale con la concavità verso l’alto.

Nel caso di una differenza di temperatura avviene, come per gli stimoli biologici, che un dislivello grosso provoca una risposta violenta.

3.   Un altro errore comune è la valutazione sulla convenienza di tenere lo scaldabagno sempre acceso.

• se lo scaldabagno è perfettamente isolato tenerlo sempre acceso o accenderlo in caso di necessità  è la stessa cosa.
• se non c’è isolamento perfetto, l’energia che devo mettere per scaldare nuovamente l’acqua è comunque quella che perdo per dissipazione; la dissipazione aumenta quando la differenza di temperatura tra acqua e ambiente sale, quindi conviene accendere solo quando serve.