APPROFONDIMENTO 2:
l'illuminamento E di una sezione del cono perpendicolare all'asse risulta inversamente proporzionale al quadrato della distanza


Consideriamo una sorgente puntiforme cioè un punto-sorgente nello spazio vuoto o in un mezzo omogeneo; l'emissione è costante nel tempo e simmetrica intorno al punto e la luce diffonde in tutto lo spazio.

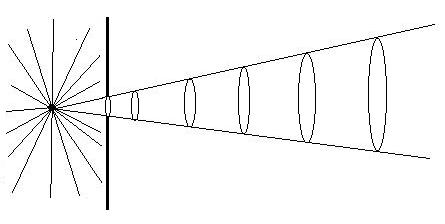Immaginiamo di porre davanti alla sorgente uno schermo con un foro circolare; oltre lo schermo passerà solo un fascio di luce con la forma di un cono con il vertice nella sorgente e la superficie laterale tangente al contorno del foro.
Consideriamo un cono di vertice S ed alcune sezioni perpendicolari al suo asse, la sua ampiezza è univocamente determinata una volta fissati il raggio (r1) del foro e la distanza (d1) dello schermo dalla sorgente.
Indichiamo con: A2, A3, …. An = le aree di sezioni circolare normali all'asse del cono
r2, r3, …. rn = i raggi delle sezioni 
d2, d3, …. dn = le distanze delle sezioni dal vertice del cono
E' possibile individuare la relazione che lega l'area delle sezioni con la loro distanza dal vertice (ripreso da supporto didattico all'esperienza 4.2 dell'unità sull'intensità luminosa):
distanza
raggio
area del cerchio
rapporto tra
raggio e r1
rapporto tra
distanza e d1
rapporto tra
area e A1
d1
r1
A1= p r12
1
1
1
d2= 2d1
r2= 2r1
A2= p r22= 4p r12
r2/r1=2r1/r=2
1/2
1/4
d3= 3d1
r3= 3r1
A3= p r32= 9p r2
r3/r1=3r1/r=3
1/3
1/9
dn= nd1
rn= nr1
An= p rn2= n2 p r2
Rn/r1=3r1/r=n
1/n
1/n2
Scriviamo la proporzione, ricavata dalla tabella precedente: 
A1: An = d12: dn2 ; 
ricaviamo An: 
An = (A1·dn2) / d12 = (A1/d12)·dn2; 
A1/d12 è un rapporto costante (cioè non dipende da n), che chiamiamo h; quindi: 
An = h·dn2 h = A1/d12
Abbiamo ottenuto due indicazioni:
  • L'area della sezione del cono normale al suo asse è proporzionale al quadrato della sua distanza dal vertice del cono: A = h·d2con h=A1/d12 (*)
  • La costante h dipende solo dalla dimensione del foro sullo schermo e dalla distanza di questo dalla sorgente ed è quindi legata univocamente all'ampiezza dell'angolo al vertice del cono. 
    		•
    L'illuminamento E di una sezione del cono perpendicolare all'asse è definito dal rapporto tra la potenza P emessa dalla sorgente all'interno del cono e l'area A della sezione:
    E = P/A
    Utilizzando la relazione (*) si ricava che l'illuminamento diminuisce con il quadrato della distanza dalla sorgente:
    E =P/(hd2)
    Essendo P e h costanti:
    E =cost/d2
    l'illuminamento E di una sezione del cono perpendicolare all'asse risulta inversamente proporzionale al quadrato della distanza dal vertice.
    Indice: