L'esperienza quotidiana ci suggerisce che ci sono sorgenti più "intense" e sorgenti più "deboli";
- alcune lampadine fanno meno luce di altre
- muovendo il regolatore di una lampada alogena è possibile variare l'intensità della luce emessa.

Tuttavia se vogliamo valutare quantitativamente:
- quanta energia emette una sorgente
- quanta dell'energia emessa può essere raccolta con un sensore
 occorre tenere presenti alcuni aspetti non immediatamente suggeriti dall'esperienza quotidiana.

I sensori di luce e quindi anche il nostro occhio, quando vengono colpiti dalla radiazione luminosa, forniscono una risposta la cui intensità (ampiezza) dipendente:

- dalla quantità di energia trasportata dalla radiazione
- dalla sua lunghezza d'onda
- dall'estensione della superficie del sensore esposta allo stimolo.

A seconda che si valuti un aspetto o l'altro di questa complessa interazione si definiscono ed utilizzano grandezze diverse.

E' necessario inoltre definire due famiglie di queste grandezze:
- grandezze energetiche definite in relazione all'energia emessa dalla sorgente o raccolta dal sensore
- grandezze fotometriche definite in relazione all'energia della radiazione, ma anche alla sua capacità di stimolare una risposta del sensore. 

Iniziamo definendo le grandezze energetiche: partiamo dall'esperienza quotidiana:
- la lampada alogena emette meno energia nella posizione di minimo rispetto a quanta ne emette nella posizione di massimo;
- tuttavia l'energia emessa dipende anche dal tempo in cui rimane accesa.

Per confrontare sorgenti diverse è necessario valutare l'energia emessa nell'unità di tempo: questa grandezza si chiama potenza (P) ed è misurata in Watt (questa grandezza viene anche chiamata flusso energetico o raggiante).

- una lampadina da 100 watt nello stesso intervallo di tempo emette più energia di una da 60 watt, quindi è più potente.

Consideriamo una sorgente puntiforme cioè un punto-sorgente nello spazio vuoto o in un mezzo omogeneo; l'emissione è costante nel tempo e simmetrica intorno al punto e la luce diffonde in tutto lo spazio.

Nessun sensore di luce è in grado di raccogliere tutta la luce emessa da questa sorgente in tutte le direzioni.
Per semplificare, immaginiamo di porre davanti alla sorgente uno schermo con un foro circolare; oltre lo schermo passerà solo un fascio di luce con la forma di un cono, con il vertice nella sorgente e la superficie laterale tangente al contorno del foro.

Piani perpendicolari all'asse del cono individuano sezioni circolari la cui area cresce all'aumentare della distanza.

A questo punto possono interessare due aspetti del problema:

1) Quanta dell'energia luminosa emessa dalla sorgente passa attraverso il foro e si propaga oltre lo schermo?
Questa quantità non dipende solo dalla potenza della sorgente, ma anche dal raggio del foro e dalla distanza dello schermo dalla sorgente.
Viene introdotta una grandezza chiamata intensità I (vedi approfondimento 1)

2) Quanta dell'energia luminosa emessa all'interno del cono può essere raccolta da un sensore?
La radiazione emessa all'interno del cono si allontana dal punto sorgente, ma si conserva.
In tempi successivi arriva a colpire sezioni del cono sempre più lontane e sempre più grandi: la stessa quantità di energia si distribuisce su superfici sempre più grandi. 
Pur conservandosi nel suo complesso, l'energia per unità di superficie è sempre più bassa, man mano che ci si allontana dalla sorgente. 

E' necessario introdurre una nuova grandezza che fornisca un'indicazione sulla "densità dell'energia" che colpisce una superficie: viene definito illuminamento E (o illuminazione) il rapporto tra il l'energia per unità di tempo (potenza P) che riceve l'elemento di superficie e la sua area A:

E = P/A

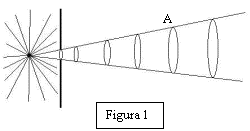
facendo riferimento al modello della figura 1 si può dimostrare (vedi approfondimento 2) che l'area (A) delle sezioni circolari aumenta in modo direttamente proporzionale al quadrato della sua distanza (d) dal vertice del cono; l'illuminamento è quindi inversamante proporzionale al quadrato della distanza:

E = k P/d²

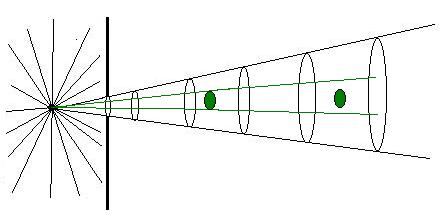
Supponiamo di porre all'interno del cono di luce di figura 1 un sensore avente un'area sensibile (S), disposta perpendicolarmente alla direzione della luce:

se spostiamo il sensore all'interno del cono di luce l'energia raccolta sarà inversamente proporzionale al quadrato della distanza dal vertice del cono.
L'energia raccolta dipende anche dall'area della superficie sensibile e dall'inclinazione del sensore (vedi approfondimento 3).

Riassumendo sono state introdotte tre grandezze:
- due si riferiscono all'energia emessa dalla sorgente: POTENZA e  INTENSITÀ
- una all'energia raccolta dal sensore: ILLUMINAMENTO

Per ogni grandezza energetica (potenza, illuminamento ed intensità) può essere definita la corrispondente grandezza fotometrica.